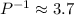Question

Six guinea pigs are released in an area with no natural predators. The guinea pig population quadruples every year. Write a function p that represents the guinea pig population at a given time t measured in years

Answer 1

Case: Exponential equation

Method:

Initial population: 6

Quadruple each year, multiplier= 4.

Where t is the number of years, the population is:

`P=6(4)^t`

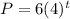
a) The inverse is calculated as:

`\begin{gathered} (P)/(6)=4^t \\ log((P)/(6))=log4^t \\ log((P)/(6))=tlog4^ \\ t=(log((P)/(6)))/(log(4)) \\ P^(-1)=(log((t)/(6)))/(log(4)) \end{gathered}`

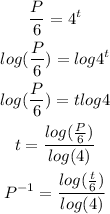
b) Approximately how long to reach 1000 guinea pigs

`\begin{gathered} P^(-1)=(log((1000)/(6)))/(log(4)) \\ P^(-1)=3.69 \end{gathered}`

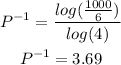
Final answers:

a)

`P^(-1)=(log((t)/(6)))/(log(4))`

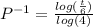
b)

`P^(-1)\approx3.7`