We know that the height of the object is given by:
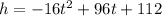
To determine when the object will hit the ground we plug h=0 and solve the equation using the quadratic formula:
![\begin{gathered} -16t^2+96t+112=0 \\ t=\frac{-96\pm\sqrt[]{(96)^2-4(-16)(112)}}{2(-16)} \\ t=\frac{-96\pm\sqrt[]{16384}}{-32} \\ t=(-96\pm128)/(-32) \\ \text{then} \\ t=(-96+128)/(-32)=(32)/(-32)=-1 \\ \text{and} \\ t=(-96-128)/(-32)=(-224)/(-32)=7 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/r2wgplz2mkqiqlzewnyn93u6pdwvm41zc8.png)
Since time has to be positve we conclude that the object will hit the ground when the time is 7 seconds.