2.6 seconds
Step-by-step explanation
we have
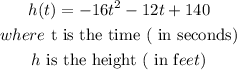
so, to knowe the time when the ball hits the ground we need to set the function equals zero and solve for t
hence
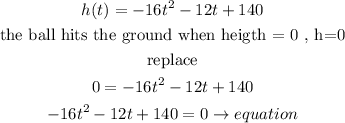
Step 2
use the quadratic formula to solve the equation:
the quadratic formula says
![\begin{gathered} \text{for} \\ ax^2+bx+c=0 \\ the\text{ solution for x is} \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/m1865iyftaresyf82yjefg3dclutiq53w9.png)
so
let
![\begin{gathered} -16t^2-12t+140=0\rightarrow ax^2+bx+c \\ so \\ a=-16 \\ b=-12 \\ c=140 \\ \text{replace in the formula} \\ t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ t=\frac{-(-12)\pm\sqrt[]{(-12)^2-4\cdot-16\cdot140}}{2\cdot-16} \\ t=(12\pm95.41)/(-32) \\ so \\ t_1=(12+95.41)/(-32)=\cdot-3.35s \\ t_1=(12-95.41)/(-32)=2.606\text{ s} \\ so\text{, the time is} \\ t=2.6\sec onds \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8c8pput3pb7ewzhx7lwfud9kxpli3gzmzc.png)
so, the answer is
2.6 seconds
I hope this helps you