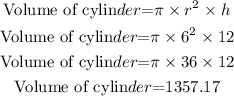As given by the question,
There are given that the sphere and cylinder.
Now,
From the formula of volume of sphere and volume of a cylinder.
Then,
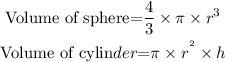
Now
Find the last two values of volume of a sphere
So,
For the volume of the sphere,
Let r be the 4cm and 6 cm.
So,
(2)
The second volume of the sphere is:

Then,
(3)
The third volume of the sphere is:

Now,
To find the volume of the cylinder, first, find the height of the cylinder
Then,
According to the question, the height of the cylinder is equal to the diameter of the sphere.
That means, for the height of the cylinder find the diameter of the sphere
So,
From the diameter of sphere
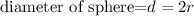
Then,
Put r=4 for second cylinder and r=6 for third cylinder
Then,

And,

Now,
Find the volume of a cylinder for second part:
So,
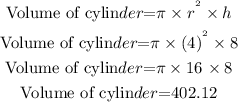
And,
For the third part: