Question

Compute the following:a. Sample meanb. Sample variancec. Sample standard deviation

Answer 1

Given:

Here a table given in the question.

Required:

a.Sample mean

b.Sample variance

c.Sample standard deviation

Step-by-step explanation:

a.Sample mean

`(\sum_^x_i)/(n)`

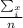
is the formula to find the sample mean

`(2+4+6+8+10+8+6+5+1)/(9)=5.56=x`

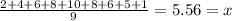
b.Sample variance

`(\sum_^(x_i-x)^2)/(n-1)=S^2`

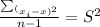
is the formula to find the sample variance

`\begin{gathered} \sum_^(x_i-x)^2=(2-5.56)^2+(4-5.56)^2+(6-5.56)^2+(8-5.56)^2+ \\ (10-5.56)^2+(8-5.56)^2+(6-5.56)^2+(5-5.56)^2+(1-5.56)^2 \\ \text{ =12.6736+2.4336+0.193+5.954+19.714+5.954+0.3136+20.793} \end{gathered}`
`\sum_^(x_i-x)^2=68.03`

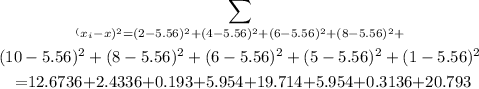
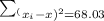
now put in formula

`S^2=(\sum_^(x_i-x)^2)/(n-1)=(68.03)/(10-1)=(68.03)/(9)=7.56`

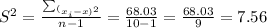
and S is the sample standard deviation

`S=\sqrt[]{7.56}=2.75`

Final Answer:

a.Sample mean=5.56

b.Sample variance=7.56

c.Sample standard deviation=2.75