Question

Two distinct lines, and m, are each perpendicular to the same line n. Select all the truestatements.

Answer 1

Given two distinct lines, l and m, each perpendicular to the same line n.

For perpendicular lines, the gradient or slope of one of the lines is the negative inverse of the other.

For instance, if

`\begin{gathered} m_1_{}\text{ is the slope of one of the perpendicular lines, the} \\ \text{slope of the other line would be }(-1)/(m_1) \end{gathered}`

Therefore,

`\text{ If the slope of line l is }m_1\text{ then the slope of line n would be }(-1)/(m_1)`

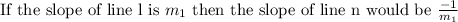
Also,

`\begin{gathered} \text{ Since line m is also perpendicular to line n, the slope of the line m} \\ \text{would be }m_1 \end{gathered}`

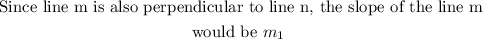
Hence, we have the following options to be correct.

B. Lines l and n are perpendicular

C. Lines m and n are perpendicular

D. Lines l and m are parallel