Question

`2a \leqslant - 4 + a`solving inequalities by multiplying and dividing

Answer 1

`2a\leqslant-4+a`

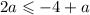
Solve the inequality for a

step 1

subtract a both sides

`\begin{gathered} 2a-a\leqslant-4+a-a \\ a\leq-4 \end{gathered}`

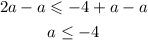
the solution is the interval for a (-infinite, -4}

Part 2

we have

`(3)/(4)t\ge9`

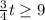
step 1

Multiply by 4 both sides

`3t\ge36`

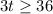
step 2

Divide by 3 both sides

`t\ge12`

the solution is the interval {12, infinite)

If you have

2a > 8

In this case, to isolate the variable a, divide both sides by 2

so

a > 8/2

a>4

If you have

2a +5 > 10

subtract 5 both sides, to isolate teh variable

2a+5-5 > 10-5

2a > 5

then

divide by 2 both sides

a > 5/2

If you have

2a > a+3

group the terms with the variable

subtract a both sides

2a-a>a+3-a

a>3

If you have

3a>a+3

group the terms with the variable

subtract a both sides

3a-a>a+3-a

2a>3

divide by 2 both sides

a>3/2