There is a fixed cost of renting and variable cost per hour.
Let fixed cost be "x" and variable costs be "y".
Saturday Cost:
x + 3y = 435
Sunday Cost:
x + 5y = 625
To find x and y, we can solve the 2 equations simultaneously. Let's multiply first equation by "-1" and add up. Shown below:
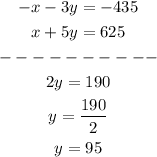
Putting this value of y into equation 2 [or equation 1 would be fine as well], we solve for x:
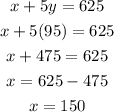
So,
fixed cost = 150 dollars
variable cost (per hour cost) = 95 dollars
Now,
Monday, he rented for 2 hours, so the cost would be:
Monday Cost:
fixed + variable (for 2 hrs)
150 + 2(95) = 340 dollars
Total Cost of Renting (for 3 days):
435 + 625 + 340 = $1400