Question

Maximize the value P=5x+5y subject to X+y < 16 X+3y< 36 , 0 0

Answer 1

We are asked to maximize the following function:

`P=5x+5y`

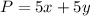
The maximum must be in the region defined by the following system of inequalities:

`\begin{gathered} x+y<16 \\ x+3y<36 \\ 00 \end{gathered}`

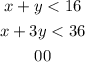
We will solve for "y" in the first inequality by subtracting "x" from both sides:

`y<16-x`

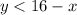
Now, we solve for "y" in the second inequality. First, by subtracting "x" from both sides:

`3y<36-x`

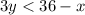
Now, we will divide both sides by 3:

`y<12-(x)/(3)`

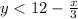
Now, we plot each of the inequalities, we get:

Now, the maximum value of the function is at one of the vertices of the region. Therefore, we substitute each of the vertices to determine the greatest value.

For (0, 0) we get:

`\begin{gathered} P(0,0)=5(0)+5(0) \\ P(0,0)=0 \end{gathered}`

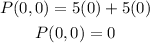
For (10,0) we get:

`\begin{gathered} P(10,0)=5(10)+5(0) \\ P(10,0)=50 \end{gathered}`

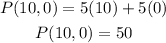
For (10,6) we get:

`\begin{gathered} P(10,6)=5(10)+5(6) \\ P(10,6)=80 \end{gathered}`

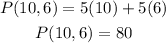
For (6,10) we get;

`\begin{gathered} P(6,10)=5(6)+5(10) \\ P(6,10)=80 \end{gathered}`

For, (0,12) we get:

`\begin{gathered} P(0,12)=5(0)+5(12) \\ P(0,12)=60 \end{gathered}`

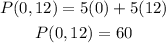
Therefore, the maximum value of the function in the given region is 80