Question

A weight is hung from the ceiling of an elevator by a massless string. Under which circumstances will the tension in the cord be the greatest?1) The elevator rises with decreasing speed.2) The elevator rises with increasing speed.3) The elevator is at rest.4) The elevator descends with increasing speed.

Answer 1

Free body diagram when the elevator is going up;

The free-body equation is given as,

`T_1-mg=ma`

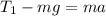
Here, T_1 is the tension in the rope while the elevator is going up, m is the mass of the body hanging from the ceiling, g is the acceleration due to gravity and a is the acceleration of the elevator.

Therefore, the tension in the rope while the elevator is going up is given as,

`T_1=ma+mg\ldots(1)`

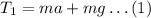
Free body diagram when the elevator is going down:

The free-body equation is given as,

`\begin{gathered} mg-T_2=ma \\ T_2=mg-ma\ldots(2) \end{gathered}`

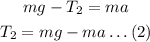
Here, T_2 is the tension in the rope while the elevator is going down.

On comparing equations (1) and (2) it is concluded that,

`T_1>T_2`

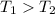
Therefore, the tension in the cord is the greatest when the elevator rises with increasing speed. Hence, option (2) is the correct choice.