Question

Find the mean and standard deviation for the probability distribution below.

Answer 1

Step-by-step explanation:

We'll go ahead and complete the 3rd column(xPr(x)) as seen below;

`\begin{gathered} 0*0.35=0 \\ 1*0.25=0.25 \\ 2*0.22=0.44 \\ 5*0.18=0.90 \end{gathered}`

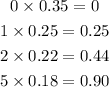
The mean can be determined using the below formula;

`\begin{gathered} \text{Mean(}\mu)=\sum ^{}_{}x\cdot Pr(x)_{} \\ \mu=0+0.25+0.44+0.90=1.59 \\ \mu=1.59 \end{gathered}`

Let's now complete the 4th column(x^2P(x)) as seen below;

`\begin{gathered} 0^2*0.35=0 \\ 1^2*0.25=0.25 \\ 2^2*0.22=0.88 \\ 5^2*0.18=4.5 \\ \sum ^{}_{}x^2.P(x)=0+0.25+0.88+4.5=5.63 \end{gathered}`

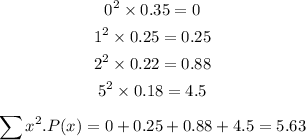
We'll use the below formula to determine the standard deviation;