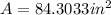Question

A regular pentagon has side lengths of 7 inches. What is the area of the pentagon?

Answer 1

The area of a regular pentagon is equal to one half the apothem times its perimeter, that is,

`A=(1)/(2)a* P`

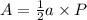
since each side has length of 7 inches and the pentagon has 5 sides, the perimeter is given by

`\begin{gathered} P=(7\text{inches)}*5 \\ P=35\text{ in} \end{gathered}`

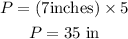
Then, in order to obtain the apothem, let's draw a picture of the pentagon:

where a denotes the apothem, which is the altitude of the right traingle from below:

So, we can relate the apothem with the side of 3.5 inche and the angle of 36 degrees by means of the tangent function, that is,

`\tan 36=(3.5)/(a)`

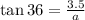
then,

`a=(3.5)/(\tan 36)`

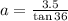
which gives

`\begin{gathered} a=(3.5)/(0.7265) \\ a=4.8173\text{ inches} \end{gathered}`

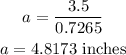
By substituting the perimeter and this result into the area formula, we have

`\begin{gathered} A=(1)/(2)a* P \\ A=(1)/(2)4.8173*35 \end{gathered}`

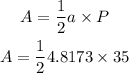
Then, the answer is:

`A=84.3033in^2`