Let the initial intensity be I, then,
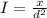
Here, x is the proportionality constant and d is the distance.
When the seat is changed o one that is thrice as far from the
speakers, we have the new intensity as,
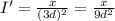
Therefore, the new intensity in terms of the original intensity can be written as,
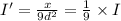
Thus, the required fraction is 1/9.