Question

The length of DE is ? and m angle cab is blank degrees

Answer 1

The length of DE = 4.5 units and m∠CAB = 45°

Step-by-step explanation:

Given:

AB = BC

D and E are midpoints of AB and BC.

Hence, DE will be the midsegment of CA

We will apply the formula for midsegment of triangle to get DE

Midsegment formula:

`\begin{gathered} DE\text{ = }(1)/(2)(CA) \\ \end{gathered}`
`\begin{gathered} CA\text{ = 9 units} \\ DE\text{ = }(1)/(2)(9) \\ DE\text{ = 4.5 units} \end{gathered}`

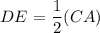
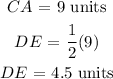
m∠ABC = 90°

Since AB = BC, the triangle is an isosceles triangle.

As a result, the base angles will also be the same

∠CAB = ∠BCA

∠ABC + ∠CAB + ∠BCA = 180° (sum of angles in a triangle)

∠ABC + ∠CAB + ∠CAB = 180°

90 + 2∠CAB = 180

2∠CAB = 180 - 90

2∠CAB = 90

Divide both sides by 2:

∠CAB = 90/2

∠CAB = 45°

If the length CA is 9 units, the length of DE is 4.5 units and m∠CAB is 45°