Given,
The number of administrators in the school is 4.
The number of teachers in the school is 32.
The number of staff member in the school is 5.
The number of member required for the committee is 3.
The total number of memebrs in the school is,
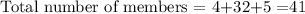
The number of ways selecting three members from the teachers is,
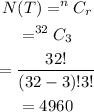
The number of ways selecting three members from all members is,
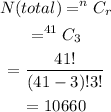
The probability that all 3 members are teachers is,

Hence, the probability that all 3 members are teachers is 0.465291.