Question

Given that f(x) is even and g(x) is odd, determine whether each function is even, odd, or neither.(f•g)(x) =?a. oddb. evenc. neither(g.g)(x)=?a. evenb. oddc. neither(f o g)(x)=?(g o g)(x)=?

Answer 1

Answers:

(f•g)(x) is odd

(g•g)(x) is even

(f o g)(x) is even

(g o g)(x) is odd

Step-by-step explanation:

If f(x) is even, then f(x) = f(-x) and if g(x) is odd, then g(-x) = -g(x)

(f•g)(x) is equal to:

(f•g)(x) = f(x)g(x)

To know if it is even or odd, we need to find (f•g)(-x), so we get:

`\begin{gathered} \mleft(f\cdot g\mright)\mleft(-x\mright)=f(-x)\cdot g(-x) \\ \mleft(f\cdot g\mright)\mleft(-x\mright)=f\mleft(x\mright)\cdot(-g(x)) \\ (f\cdot g)(-x)=-f(x)g(x) \\ (f\cdot g)(-x)=-(f\cdot g)(x) \end{gathered}`

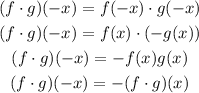
Since (f•g)(-x) = -(f•g)(x), the function is odd.

In the same way, (g.g)(x) is equal to:

`(g\cdot g)(x)=g(x)g(x)`

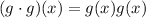
Therefore, (g.g)(-x) is:

`\begin{gathered} (g\cdot g)(-x)=g(-x)\cdot g(-x) \\ (g\cdot g)(-x)=(-g(x))\cdot(-g(x)) \\ (g\cdot g)(-x)=g(x)\cdot g(x) \\ (g\cdot g)(-x)=(g\cdot g)(x) \end{gathered}`

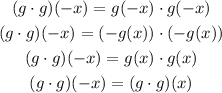
So, the function (g.g)(x) is even.

On the other hand, the composite function (f o g)(x) is equal to:

(f o g)(x) = f( g(x) )

So, (f o g)(-x) si equal to:

`\begin{gathered} (f\text{ o g)(-x) = f(g(-x))} \\ (f\text{ o g)(-x) =f}(-g(x)) \\ (f\text{ o g)(-x) = f(g(x))} \\ (f\text{ o g)(-x) = (f o g)(x)} \end{gathered}`

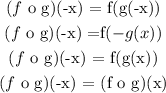
Therefore, (f o g)(x) is even

Finally, (g o g)(x) is equal to:

(g o g)(x) = g( g(x) )

Then, (g o g)(-x) is equal to:

`\begin{gathered} (g\text{ o g)(-x) = g ( g(-x))} \\ (g\text{ o g)(-x) = g( -g(x))} \\ (g\text{ o g)(-x) = }-g(g(x)) \\ (g\text{ o g)(-x) =}-(g\text{ o g)(x)} \end{gathered}`

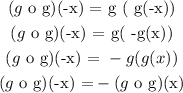
Therefore, (g o g)(x) is odd.