Rate of change
Exponential functions increase faster than linear functions because the variable is at the exponent.
We have two exponential functions and two linear functions.
The exponential functions are
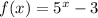
And
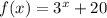
We can compare which of the exponential function grow faster by substituting x for two values.
Select x=1 and x=2
The first equation for both values is:

Now for the second function:
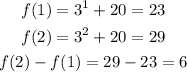
Therefore, the function that increases the fastest is
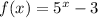
you cannot see the messages?
no problem, let's talk from here
did you follow the above explanation?
ok now we only have to compare both exponential functions
The answer is complete
Hope I could help you
Did you understand the explanation?
You are very welcome!
Feel free to let me know how I did by rating our session once you close it
Have a great rest of your day!
do you want me to close the session?