Question

triangle IJK with vertices I(-9,-8),(J-5,-6), and K(-7,-3), is drawn on the coordinate grid below. what is the area in square units of triangle IJK

Answer 1

First, we have to calculate the length of each side using the distance formula.

Given two points (x1, y1) and (x2, y2) the distance between them is computed as follows:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Segment IJ: I(-9, -8) and J(-5,-6)

`\begin{gathered} IJ=\sqrt[]{(-5-(-9))^2+(-6-(-8))^2} \\ IJ=\sqrt[]{16+4^{}} \\ IJ=\sqrt[]{20^{}}\approx4.47 \end{gathered}`

Segment IK: I(-9, -8) and K(-7,-3)

`\begin{gathered} IK=\sqrt[]{(-7-(-9))^2+(-3-(-8))^2} \\ IK=\sqrt[]{4+25} \\ IK=\sqrt[]{29}\approx5.39 \end{gathered}`

Segment JK: J(-5, -6) and K(-7,-3)

`\begin{gathered} JK=\sqrt[]{(-7-(-5))^2+(-3-(-6))^2} \\ JK=\sqrt[]{4+9} \\ JK=\sqrt[]{13}\approx3.61 \end{gathered}`

Using Heron's formula,

`\begin{gathered} s=(IJ+IK+JK)/(2) \\ s=(4.47+5.39+3.61)/(2) \\ s=6.74 \end{gathered}`
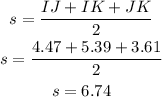
`\begin{gathered} \text{Area}=\sqrt[]{s\cdot(s-IJ)\cdot(s-IK)\cdot(s-JK)} \\ \text{Area}=\sqrt[]{6.74\cdot(6.74-4.47)\cdot(6.74-5.39)\cdot(6.74-3.61)} \\ \text{Area}=\sqrt[]{6.74\cdot2.27\cdot1.35\cdot3.13} \\ \text{Area}=\sqrt[]{64.65} \\ \text{Area=}8.04\text{ square units} \end{gathered}`