Since the acceleration on the y-axis is 0, then the movement in the vertical direction can be modeled as a constant speed motion:
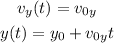
On the other hand, since the acceleration on the x-axis is different from 0 and it is a constant acceleration, then, the horizontal movement of the particle can be modeled as a uniformly accelerated motion:
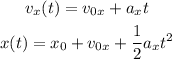
Part a)
Since the particle is at the origin at t=0, then x₀=0 and y₀=0.
Replace v_0x=0, v_0y=6.4m/s and a_x=-4m/s^2 into the equations to find the expressions for x(t), y(t), v_x(t) and v_y(t):
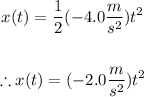
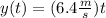
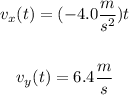
Evaluate the expressions for x(t) and y(t) at t=4.5s to find the x and y positions of the particle at t=4.5s:
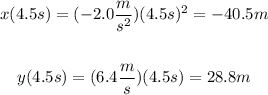
Part b)
Replace t=4.5s into the expressions for the velocities of the particle to find v_x and v_y at t=4.5s:
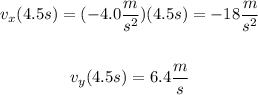
Part c)
Initially, the horizontal component of the velocity was 0 while the vertical component of the velocity was 6.4m/s. After 4.5 seconds, the vertical component of the velocity stays the same but the horizontal component changes to -18m/s. The magnitude of the velocity increases because the magnitude of one of the components increases while the other remains the same.
Therefore, the answers are:
Part a)
x = -40.5 m
y = 28.8 m
Part b)
v_x = -18 m/s
v_y = 6.4 m/s
Part c)
The particle's speed increases with time.