Let the age of students in a certain public high school be x;
So, we create a table of values as follows;
First, we fine the mean of the distribution, we have;
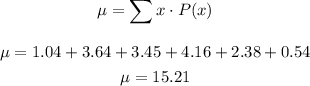
Thus, the standard deviation of the distribution is;
![\sigma=\sqrt[]{\sum^{}_{}(x_i-\mu)^2* P(x_i)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wx9ph13jablricssfmbfows4ssh2360vik.png)
Then, we will insert the deviation in the table above,
Then, we have;
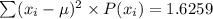
![\begin{gathered} \sigma=\sqrt[]{1.6259} \\ \sigma=1.2751 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/lj0qu1y8jo5tm1oyyasmcbbia54or47c67.png)
The standard deviation of the ages is 1.2751
Also, the variance is;
The variance is the square of standard deviation, we have;
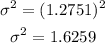
Thus, the variance of the ages is 1.6259