Question

List the possible rational roots of the equation & solve:y^4 - 3y^3 - 2y^2 + 10 y - 12= 0

Answer 1

Given:

`y^4-3y^3-2y^2+10y-12=0`

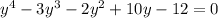
Required:

We need to find roots of the equation.

Step-by-step explanation:

`\text{ The factors of 12 are P= \textbraceleft}\pm1,\pm2,\pm3,\pm4,\pm6,\pm12\rbrace`
`The\text{ factors of 1 are Q=\textbraceleft}\pm1\rbrace`
`(P)/(Q)=P=\text{\textbraceleft}\pm1,\pm2,\pm3,\pm4,\pm6,\pm12\rbrace`

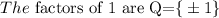
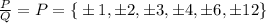
The possible roots of the equation are

`\text{\textbraceleft}\pm1,\pm2,\pm3,\pm4,\pm6,\pm12\rbrace`

Let y =1 and substite int the equation.

`(1)^4-3(1)^3-2(1)^2+10(1)-12=0`

`1-3-2+10-12=0`

`-6=0`

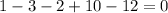
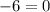
y=1 is not a root.

Let y =-1 and substitue in the equation.

`(-1)^4-3(-1)^3-2(-1)^2+10(-1)-12=0`

`1+3-2-10-12=0`

`-20=0`

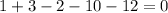
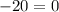
y= -1 is not a root.

Let y = 2 and substitue in the equation.

`(2)^4-3(2)^3-2(2)^2+10(2)-12=0`

`16-24-8+20-12=0`

`-8=0`

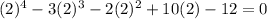
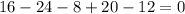
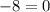
y=2 is not a root.

Let y = - 2 and substitue in the equation.

`(-2)^4-3(-2)^3-2(-2)^2+10(-2)-12=0`

`(2)^4+3(2)^3-2(2)^2-10(2)-12=0`

`16+24-8-20-12=0`
`0=0`

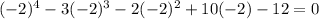
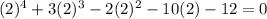
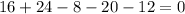
y = -2 is the root of the given equation.

Use the synthetic method to find the roots.

The given equation can be written as follows.

`(y+2)(y^3-5y^2+8y-6)=0`

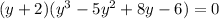
Consider the equation to find the remaining roots.

`y^3-5y^2+8y-6=0`

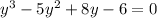
Set y = 2 ans substitute in the equation.

`(2)^3-5(2)^2+8(2)-6=0`

`8-20+16-6=0`

`-2=0`

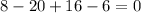
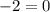
y =2 is not the second root.

Set y = -2 and substitute in the equation.

`(-2)^3-5(-2)^2+8(-2)-6=0`

`-(2)^3-5(2)^2-8(2)-6=0`

`-50=0`

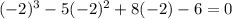
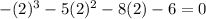
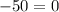
y = -2 is not the second root.

Set y = 3 and substitute in the equation.

`(3)^3-5(3)^2+8(3)-6=0`

`27-45+24-6=0`
`0=0`

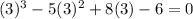
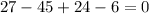
y = 3 is the second root.

Use the synthetic method.

The given equation can be written as follows.

`(y+2)(y-3)(y^2-2y+2)=0`

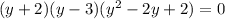
Consider the equation to find the remaining roots.

`y^2-2y+2=0`

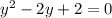
Which is of the from

`ax^2+bx+c=0`

where a =1, b=-2 and c=2.

Cnmdidr the qudaratic formuola.

`x=(-b\pm√(b^2-4ac))/(2a)`

Substitute a =1, b=-2 and c=2 in the formula.

`y=(-(-2)\pm√((-2)^2-4(2)(1)))/(2(1))`

`y=(2\pm√(4-8))/(2)`

`y=(2\pm√(i^22^2))/(2)`

`y=(2\pm2i)/(2)`
`y=1+i,1-i`

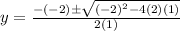
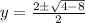
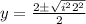
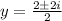
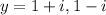
Final answer:

The roots are -2, -3,1+i and 1-i.