we have that
the area of the rectangular pen is equal to
A=L*W
A=63m2
so
L*W=63 ------> equation 1
the perimeter with 25 meters of fencing (Only three sides) is equal to
P=L+2W
L is the longer side
P=25
25=L+2W -----> L=25-2W -----> equation 2
substitute equation 2 in equation 1
(25-2W)*W=63
25W-2W^2=63
2w^2-25w+63=0
solve the quadratic equation using the formula
a=2
b=-25
c=63
substitute
![w=\frac{-(-25)\pm\sqrt[]{-25^2-4(2)(63)}}{2(2)}](https://img.qammunity.org/2023/formulas/mathematics/college/3ypaehljt6lvdb953cwour18x4jfgp9v8u.png)
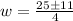
the values of w are
w=9 and w=3.5
Find out the value of L
For w=9 m
L=25-2(9)=7 m
is not the solution because L is the longer side
so
For w=3.5 m
L=25-2(3.5)=18 m
therefore
The dimensions are
Length 18 meters
Width 3.5 meters