Question

Find , , and if and terminates in quadrant .

Answer 1

sin2x =12/13

cos2x = 5/13

tan2x = 12/5

STEP - BY - STEP EXPLANATION

What to find?

• sin2x

,

• cos2x

,

• tan2x

Given:

tanx = 2/3 = opposite / adjacent

We need to first make a sketch of the given problem.

Let h be the hypotenuse.

We need to find sinx and cos x, but to find sinx and cosx, first determine the value of h.

Using the Pythagoras theorem;

hypotenuse² = opposite² + adjacent²

h² = 2² + 3²

h² = 4 + 9

h² =13

Take the square root of both-side of the equation.

h =√13

This implies that hypotenuse = √13

We can now proceed to find the values of ainx and cosx.

Using the trigonometric ratio;

`\sin x=\frac{opposite}{\text{hypotenuse}}=\frac{2}{\sqrt[]{13}}`
`\cos x=\frac{adjacent}{\text{hypotenuse}}=\frac{3}{\sqrt[]{13}}`

And we know that tanx =2/3

From the trigonometric identity;

sin 2x = 2sinxcosx

Substitute the value of sinx , cosx and then simplify.

`\sin 2x=2(\frac{2}{\sqrt[]{13}})(\frac{3}{\sqrt[]{13}})`
`=(12)/(13)`

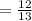
Hence, sin2x = 12/13

cos2x = cos²x - sin²x

Substitute the value of cosx, sinx and simplify.

`\begin{gathered} \cos 2x=(\frac{3}{\sqrt[]{13}})^2-(\frac{2}{\sqrt[]{13}})^2 \\ \\ =(9)/(13)-(4)/(13) \\ =(5)/(13) \end{gathered}`

Hence, cos2x = 5/13

tan2x = 2tanx / 1- tan²x

`\tan 2x=(2\tan x)/(1-\tan ^2x)`
`=(2((2)/(3)))/(1-((2)/(3))^2)`
`=((4)/(3))/(1-(4)/(9))`
`=((4)/(3))/((9-4)/(9))`
`=((4)/(3))/((5)/(9))`
`=(4)/(3)*(9)/(5)=(4)/(1)*(3)/(5)=(12)/(5)`

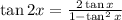
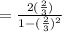
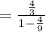
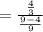
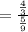
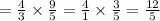
OR

`\tan 2x=(\sin 2x)/(\cos 2x)=((12)/(13))/((5)/(13))=(12)/(5)`

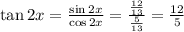
Hence, tan2x = 12/5

Therefore,

sin2x =12/13

cos2x = 5/13

tan2x = 12/5