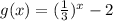ANSWER:
A)
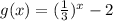
Explanation:
Given the parent function:
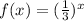
We evaluate this to zero to get the y-intercept:
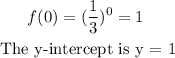
While on the graph, the y-intercept is at y = -1
Therefore, it is 2 units below the y-intercept of the parent function, which means the function is translated 2 units down. This is reflected in the equation as a subtraction of 2 units from the parent function.
Therefore, the equation would be: