Question

What is the rectangular equivalence to the parametric equations?What interval does x fall under?

Answer 1

The rectangular equivalence is:

`((x-2)/(4))^2+((y+1)/(5))^2=1`

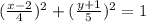
The interval of x is [-2, 6]

Step-by-step explanation:

To find the rectangular equivalence, we want an equation of the form:

`\cos^2(\theta)+\sin^2(\theta)=1`

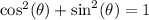
Then, we have the equations:

`\begin{gathered} x(\theta)=4\cos(\theta)+2 \\ y(\theta)=5\sin(\theta)-1 \end{gathered}`

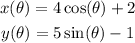
On each equation, we solve for cos and sin:

`(x-2)/(4)=\cos(\theta)`
`(x-2)/(4)=\cos(\theta)`
`(y+1)/(5)=\sin(\theta)`

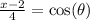
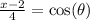
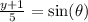
Now we can square both sides:

`\begin{gathered} ((x-2)/(4))^2=\cos^2(\theta) \\ \end{gathered}`
`((y+1)/(5))^2=\sin^2(\theta)`

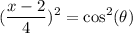
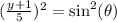
Now we can write:

`((x-2)/(4))^2+((y+1)/(5))^2=1`

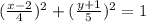
That's the rectangular equivalence of the parametric equations.

Now, to find the interval where x falls under, we have:

`x(\theta)=4\cos(\theta)+2`

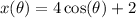
In this function, the value of x depends only on of θ. The maximum value that cos(θ) is 1, when θ = 0

Then, if θ = 0, cos(θ) = 1

`x(0)=4\cdot1+2=6`

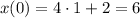
The minimum value of cos(θ) is -1, when θ = π

If θ = π, cos(θ) = -1

Then:

`x(\pi)=4\cdot(-1)+2=-2`

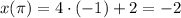
The interval is [-2, 6]