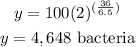A certain type of bacteria,
given a favorable growth
Medium, doubles in population every 6.5 hours. Given that there were approximately 100 bacteria to start with, how many bacteria will there be in a day and a half?
we have that
the exponential growth function that represent this situation is
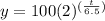
where
x is the number of hours
y is the total bacteria
so
For a day -------> t=24 hours
substitute
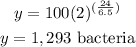
For a half day -------> t=12 hours
substitute
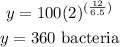
For a day and a half -------> t=36 hours
substitute