GIVEN:
We are given the following polynomial equation;
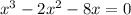
Required;
Factorize the equation.
Step-by-step solution;
We begin by taking out the common factor, and that is x;
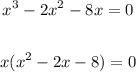
Therefore we have,
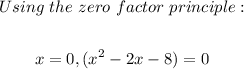
Next we factorize the expression in parenthesis;

Therefore the three factors are;

ANSWER:
