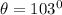Step-by-step explanation:
Given that θ is an obtuse angle and the value of the trigonometric ratio
The equation is given below as
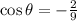
Since the angle is an obtuse angle, it greater than 90 but less than 180 degrees which means that the angle falls in the second quadrant
In the second quarant,
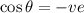
Hence,
The diagram will be given below as
Part b:
To figure out the value of
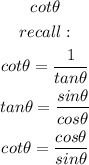
To figure value of sin theta we will calulate the opposite using pythagoras theorem below
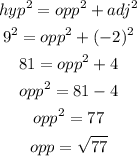
Hence,
The value of sin theta will be
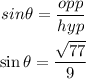
Hence,
The value of cot theta will be
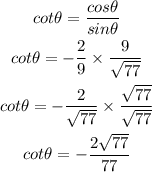
Hence,
The value of cot theta is
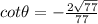
Part C:
To determine the value of theta
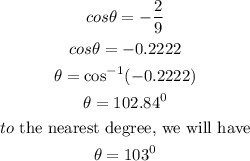
Hence,
The value of θ to the nearest degree is