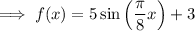Question

NO LINKS!! Please help me with this problem Part 2e​

Answer 1

`\textsf{b)} \quad f(x)=5 \sin\left((\pi)/(8)x\right)+3`

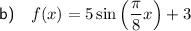
Explanation:

Standard form of a sine function

`f(x)=\text{A} \sin\left[\text{B}(x+\text{C})\right]+\text{D}`

where:

• A = amplitude (height from the mid-line to the peak).
• 2π/B = period (horizontal distance between consecutive peaks).
• C = phase shift (horizontal shift - positive is to the left).
• D = vertical shift.

Given:

• Period = 16 units
• Mid-line: y = 3
• Maximum: y = 8

If the maximum is y = 8 and the mid-line is y = 3 then the amplitude is:

`\implies A=8-3=5`

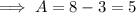
If the period is 16 units then:

`(2\pi)/(B)=16 \implies B=(2\pi)/(16)=(\pi)/(8)`

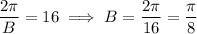
There appears to be no horizontal shift, so C = 0.

If the mid-line is y = 3 then the curve has been shifted 3 units up (vertically). Therefore, D = 3.

Substitute these values into the standard formula:

`\implies f(x)=5 \sin\left[(\pi)/(8)(x+0)\right]+3`

`\implies f(x)=5 \sin\left((\pi)/(8)x\right)+3`