Question

A bicycle has a wheel with a diameter of 2 feet How far does the bike roll if the wheel makes a rotation of 90 degrees ? How far does the bike roll if the wheel makes 10 rotations ?

Answer 1

The circumference of a circle of radius r is given by:

`C=2\pi r`

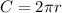
This represents the length rolled by the circle when it makes one full rotation. If it makes an angle of θ radians, the length is:

`L=\theta r`

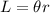
a) It's required to calculate the length rolled by the bicycle when it rotates 90 degrees. We need to convert degrees to radians as follows:

`\theta=90\cdot(\pi)/(180)=(\pi)/(2)`

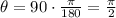
The radius of the bicycle is half the diameter:

r = 2 feet / 2 = 1 feet.

Calculate L:

`\begin{gathered} L=(\pi)/(2)\cdot1\text{ feet} \\ L=(\pi)/(2)\text{ feet} \end{gathered}`

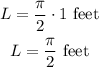
The question does not specify the format of the answer, so we also provide an approximate answer below:

L ≈ 3.14 / 2 = 1.57 feet

b) The length of one rotation is:

`\begin{gathered} C=2\pi(1\text{ foot}) \\ C=2\pi\text{ feet} \end{gathered}`

For 1'0 rotations:

`\begin{gathered} C=10\cdot2\pi\text{ feet} \\ C=20\pi\text{ feet} \end{gathered}`

Approximating C ≈ 20 x 3.14 = 62.8 feet