Question

() = −2| − 1| + 2 Select all the transformations applied to the absolute value toolkit function.- Stretched vertically by a factor of 2.- Translated to the right 1 unit.- Reflected over the x-axis.- Translated up 2 units.- Translated to the left 1 unit.

Answer 1

- Stretched vertically by a factor of 2

- Translated to the right 1 unit

- Reflected over the x-axis

- Translated up 2 units

Step-by-step explanation

We want to identify all the transformations for the given absolute value function:

`f(x)=-2\lvert{x-1}\rvert+2`

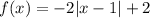
The parent function for absolute value functions is:

`f(x)=\lvert{x}\rvert`

The function was first multiplied by 2:

`f(x)=2\lvert{x}\rvert`

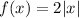
This represents a vertical stretch by a factor of 2.

Then, the function was multiplied by -1:

`f(x)=-2\lvert{x}\rvert`

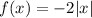
This represents a reflection over the x-axis.

Then, the function was transformed as follows:

`f(x)=-2\lvert{x-1}\rvert`

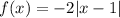
This represents a horizontal translation to the right by 1 unit.

And finally, it was transformed as follows:

`f(x)=-2\lvert{x-1}\rvert+2`

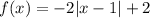
This represents a vertical translation up by 2 units.

Hence, the transformations that the function underwent are:

- Stretched vertically by a factor of 2

- Translated to the right 1 unit

- Reflected over the x-axis

- Translated up 2 units