Question

Square root of (x+1) - square root of (x-2) =5. Solve for x

Answer 1

We have to solve the expression:

`√(x+1)-√(x-2)=5`

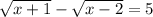
We can start by finding the domain of possible values of x.

The argument of the square root can not be negative, so we can limit the values of x as:

`\begin{gathered} 1)\text{ }x+\geq0 \\ x\geq-1 \\ 2)\text{ }x-2\geq0 \\ x\geq2 \end{gathered}`

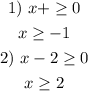
Then, x has to be greater than 2, as this interval is more restrictive.

When x gets very large, the difference between the two roots approaches 0.

Also, the difference of this square roots decreases with the increase of x, so the maximum value happens for x = 2, which is the minimum value of x in the domain.

We then can calculate the value for the difference of square roots when x = 2 as:

`\begin{gathered} √(2+1)-√(2-2) \\ √(3)-√(0) \\ √(3)<5 \end{gathered}`

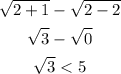
Then, one side of the equation has a maximum value that is the square root of 3. This maximum value is already smaller than 5, so there is no value of x that can make this expression equal to 5.

Answer: there is no solution for x.