ANSWER
179 ft
Step-by-step explanation
Let us draw a simplified diagram of the problem:
We first have to find H.
Let us split the triangle into two, to make it simpler:
To find H from the smaller triangle, use trigonometric functions SOHCAHTOA.
We have that:
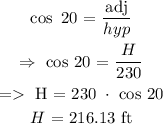
Now, we need to find G, because the height of the tree is:
height of tree = T - G
From the smaller diagram, using SOHCAHTOA:

So, now, we use the big triangle to find T by using SOHCAHTOA:
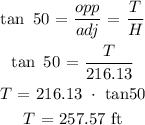
Therefore, the height of the tree is:
height = 257.57 - 78.66
height = 178.91 ft
To the nearest foot, the height of the tree is 179 ft.