Question

X-1=square root of 4x-4

Answer 1

Given the equation:

`x-1=\sqrt[]{4x-4}`

Let's solve the equation for x.

To solve for x, take the following steps:

• Step 1.

Square both sides:

`\begin{gathered} (x-1)^2=\sqrt[]{4x-4}^2 \\ \\ (x-1)(x-1)=4x-4 \\ \end{gathered}`

• Step 2.

Expand using FOIL method and distributive property

`\begin{gathered} x(x-1)-1(x-1)=4x-4 \\ \\ x(x)+x(-1)-1(x)-1(-1)=4x-4 \\ \\ x^2-x-x+1=4x-4 \\ \\ x^2-2x+1=4x-4 \end{gathered}`

• Step 3.

Add 4 to both sides and also subtract 4x from both sides:

`\begin{gathered} x^2-2x-4x+1+4=4x-4x-4+4 \\ \\ x^2-6x+5=0 \end{gathered}`

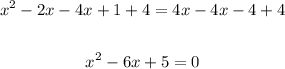
• Step 4.

Factor the left side of the equation using the AC method.

Find two numbers whose sum is -6 and whose product is 5.

Thus, we have:

-5 - 1 = -6

-5 x -1 = 5

Therefore, the numbers are:

-5, and -1

Hence, we have:

`(x-5)(x-1)=0`

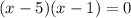
Equate trhe individual factors to zero and solve for x:

`\begin{gathered} x-5=0 \\ \text{Add 5 to both sides}\colon \\ x-5+5=0+5 \\ x=5 \\ \\ \\ x-1=0 \\ \text{Add 1 to both sides:} \\ x-1+1=0+1 \\ x=1 \end{gathered}`

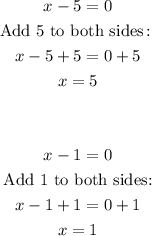
Therefore, the solutions to the given equation is:

`x=5,\text{ and 1}`

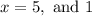
ANSWER:

x = 5, 1