Answer:
D. Increases by 35.2%
Explanation:
Let the initial radius and height be r and h respectively.
So, the volume (V) is:
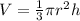
When radius increases by 30%.
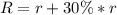
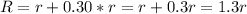
When height decreases by 20%.
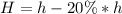
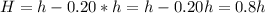
So, the new volume V2 is:
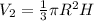
This gives:
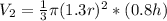
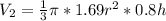
Rewrite as:
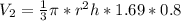
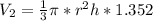
Rewrite as:
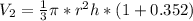
Express as percentage:
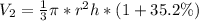
This implies that the volume increases by 35.2%