SOLUTION
Part A.
Wrtite out the function given
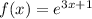
A functionn g(x) is the inverse of f(x) if for y=f(x), x=g(y).
To obtain the inverse of f(x), replace f(x)=y, we have
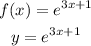
Isolate x in the equation above
take logarithm of both sides
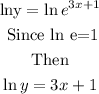
Subrtract 1 from both sides, we have
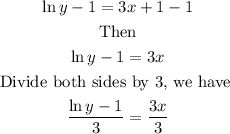
Then
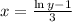
Then the inverse of the function becomes
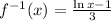
Hence
The inverse of the function, f(x) is
f¹(x)=ln x - 1 / 3
The Domian of a function are the set of the input value of for which the function is defined or real.
Hence
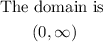
Therefore
The domain fo the inverse of f(x) is (0, ∞)
Part B
The function g(x) is given as
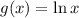
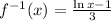
The point of intersection is the point where
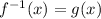
Then, we have

Then, subtract both sides by ln x
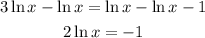
Divide both sides with 2 we have
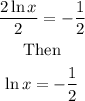
Then, take the exponent of both sides, we have
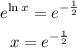
Then
![\begin{gathered} x=\frac{1}{e^{(1)/(2)}}=\frac{1}{\sqrt[]{e}} \\ \text{Hence } \\ x=\frac{1}{\sqrt[]{e}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9xy7bv1opkvq5a03onlo3b30hefwkljwkx.png)
Then substitute the value of x into g(x) to find y, we have \
From the question,
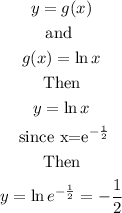
Therefore the point of intersection P is
![(\frac{1}{\sqrt[]{e}},-(1)/(2))](https://img.qammunity.org/2023/formulas/mathematics/college/xmodhrmf7aadebe7tzyjtfbndbsl3ph9zr.png)
Consider the graph below
Therefore point P is (0.607, -0.5)