We are given that two trains start a distance of 992 km apart. If they meet after 4 hours, this means that the sum of the distances of both trains after 4 hours traveling must be 992 km. This is written mathematically as:
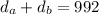
Now, the distance traveled by an object is given by the following relationship:
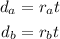
Where:
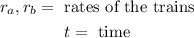
Now, we substitute the values in the equation for the total distance:
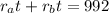
Now, the time is 4 hours, therefore, we have:
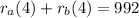
Now, we are also given that one train travels 20 km/h slower than the other. If a is the slower train then we have:
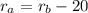
Substituting we get:
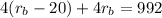
Now, we divide both sides by 4:
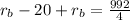
Solving the operations:

Now, we add like terms:
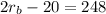
Now, we add 20 to both sides:
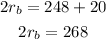
Now, we divide both sides by 2:
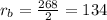
Therefore the fastest train has a rate of 134 km/h. Now, we determine the rate of the slower train:
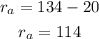
Therefore, the slower train travels ar 114 km/h