Question

Solve and Graph let f (x) = 5 + | 2x -5 | Find all x for which f (x< 26

Answer 1

We have the function:

`f(x)=5+|2x-5|\text{.}`

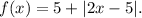
We must find all the x for which we have:

`f(x)<26.`

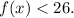
1) Replacing the definition of f(x) in the inequality, we have:

`5+|2x-5|<26.`

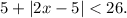
2) Solving for x, we get:

[tex]\begin{gathered} |2x-5|<26-5, \\ |2x-5|<21, \\ -21<2x-5<21, \\ -21+5<2x<21+5, \\ -16<2x<26, \\ -\frac{16}{2}The solution is the set of values of x that are greater than -8 and smaller than 13. In interval notation: (-8, 13).

Plotting the points, we get the following graph:

Answer

• The solution are the values of x such that: ,-8 < x < 13,.

,

• Or the points in the interval ,(-8, 13),.

,

• Graph