
1) The best way to tackle this question is to think of rational equations. Since, time, rate and distance are related.
2) So, we can start writing the following:
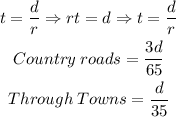
So, let's solve it by equating the sum of these expressions to the spent time: 4 hours (common to both)
Now we have the LCM
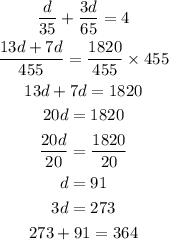
Note that adding them up, the distance in country roads and the distance in towns.