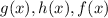Solution:
The rate of change, m, of a function f is;
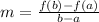
Given the graph, f(x);
Its rate of change over the given interval is;
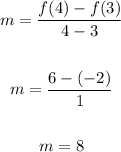
Given the table of g(x);
Its rate of change over the interval is;
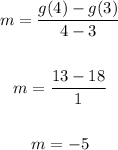
Also, given the function of h(x);
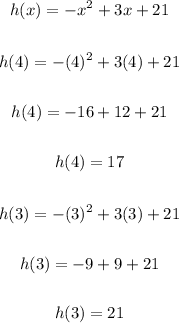
Its rate of change over the interval is;
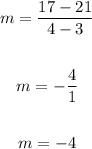
The order of the rate of change from the least to the greatest is;
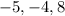
CORRECT OPTION: