Question

F(x) = ( x-a)(x-b)T(x)= (x-c)(x-d)J(x)= F(x)/T(x)If a≠b≠c≠d then which two functions have the same set of zeros?

Answer 1

Recall that:

1) The zeros of a polynomial function of the form:

`p(x)=(x-a_1)\cdot\ldots\cdot(x-a_n)`

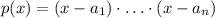
are:

`a_1,\ldots,a_n\text{.}`

2) The set of zeros of a rational function of the form:

`r(x)=((x-a_1)\cdot\ldots\cdot(x-a_n))/((x-b_1)\cdot\ldots\cdot(x-b_m))`

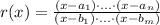
is:

`\mleft\lbrace a_1,\ldots,a_n\mright\rbrace\text{ \backslash }\mleft\lbrace b_1,\ldots,b_m\rbrace\mright?.`

Therefore the zeros of F(x) are a and b, the zeros of T(x) are c and d.

Finally, since

`a\\e b\\e c\\e d,`

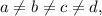
then the zeros of J(x) are a and b.

Answer: F(x) and J(x) have the same set of zeros.