We have to find an expression for the total cost T. It will be the sum of the cost of manufacturing, storing and the fixed daily cost.
We know that the cost of manufacturing Cm is proportional to the quantity n. This also means that the quotient Cm/n is constant:
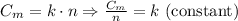
We also know that when the quantity is n = 800, the cost of manufacturing is Cm = 240,000. Then, we can calculate the constant as:
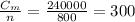
Then, we can express the cost of manufacturing in function of the number of units n as:
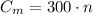
Now, we know that the cost of storing Cs is protopotional to the square of the quantity, n². This can be written as:
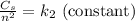
As the cost of storing is Cs = 6,400 when n = 800. Then, we can relate Cs to n as:
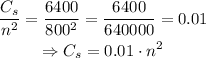
Finally, we have a fixed cost of $4000 per day, that does not depends on n:
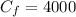
Then, we can now express the total cost T as a function of n as the sum of this partial costs:
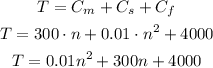
Answer: T = 0.01n² + 300n + 4000