We know that a parabolla is given by the form:
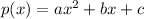
We also know that we can factor this equation to get the form:

Where
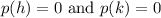
This is, h and k are the roots.
Then we can write:
h = 14
k = 11
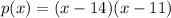
We can also doing the multiplication to give the answer is standard form a parabolla:
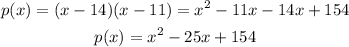
And that's a function as aked in the problem.