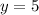Answer:
Step-by-step explanation:
Here, we want to write the equation of a line in both the standard and slope-intercept form
The general form is the slope-intercept form which is
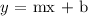
where m is the slope and b is the y-intercept
From the equation given, we have it that the slope is 0
When two lines are parallel, the value of their slopes is equal
Thus, the slope of the line we want to write its equation is 0 too
For the slope-intercept form:
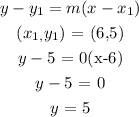
This is the slope-intercept form
The general form is:
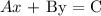
There is no parts for x since the slope is zero
Thus, we have the standard form as: