Question

Are the triangles similar if so complete the Similarity and state how you know they are similar.

Answer 1

First of all it's important to note a few things. Angles SBT and DBC are opposite angles in the intersection of two straight lines. This means that they have the same measure so:

`\angle SBT=\angle DBC`

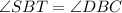
Then let's take a look to the ratios between these sides:

`\begin{gathered} (BC)/(DB)=(121)/(176)=(11)/(16) \\ (BS)/(TB)=(44)/(64)=(11)/(16) \end{gathered}`

So the ratios are the same. This allow us to associate sides of one triangle with sides of the other:

`\begin{gathered} BC\leftrightarrow BS \\ DB\leftrightarrow TB \end{gathered}`

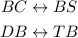
Which also means that we can associate the following vertices:

`\begin{gathered} D\leftrightarrow T \\ C\leftrightarrow S \end{gathered}`

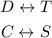
Now let's recal the SAS similarity theorem:

"When you've got two triangles and the ratio of two of their sides are the same, plus one of their angles are equal then the triangles are similar"

As we showed before they share a triangle and the ratio of two of their sides are the same so by SAS these triangles are similar. Using the association of vertices we get:

`\Delta BCD\approx\Delta BST`

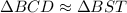
Then the answer is the first option.