Given that the sum of 2 numbers is 1 and their product is 1, let's find the sum of their cubes.
Let x and y represent the numbers.
Thus, we have:
x + y = 1..........................equation 1
x y = 1...........................equation 2
Here, we are to find x³ + y³ .
Thus, we can write this as:
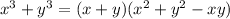
Manipulating this, we can write:
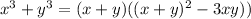
Substitute the values for x+y and xy into the equation above, we have:
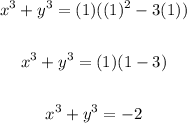
Therefore, the sum of their cubes is -2.
ANSWER:
-2