We have 2 equations of straight lines which are:
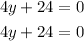
The first thing we will do is to clear the unknowns of both equations, as follows:
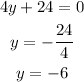
This represents a horizontal line since it is considered to have zero slopes. The horizontal line is the one whose trajectory represents the direction of the horizon as we perceive it. It moves from right to left and vice versa, being also perpendicular (at an angle of 90º).
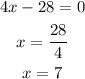
This represents a vertical line since it is considered to have an infinite slope, vertical lines are those whose trajectory is up-down and vice versa.
In conclusion, Since the equations represent a horizontal line and a vertical line, forming a 90-degree angle they are perpendicular.