Given:
• q1 = -4.60 x 10⁻⁶ C.
,
• q2 = +3.75 x 10⁻⁶ C.
,
• q3 = +8.30 x 10⁻⁵ C.
,
• d12 = 0.283 m
,
• d23 = 0.200 m
,
• d13 = 0.200
Let's find the magnitude of the net force on q3.
Let's first find the force acting on q1 and q3:
![\begin{gathered} F_(13)=(kq_1q_2)/((d_(13))^2) \\ \\ F_(13)=\frac{9*10^9*4.60\operatorname{*}10^(-6)*8.30\operatorname{*}10^(-5)}{0.200^2} \\ \\ F_(13)=85.9\text{ N} \end{gathered}]()
Also, for the force acting on q2 and q3, we have:
![\begin{gathered} F_(23)=(kq_2q_3)/((d_(23))^2) \\ \\ F_(23)=\frac{9*10^9*3.75\operatorname{*}10^(-6)*8.30\operatorname{*}10^(-5)}{0.200^2} \\ \\ F_(23)=70.03\text{ N} \end{gathered}]()
Therefore, the magnitude of the net force on q3 will be:
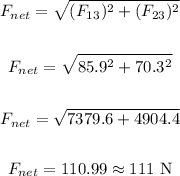
Therefore, the magnitude of the net force on q3 is 111 N.
• ANSWER:
111 N