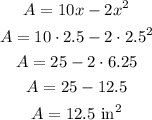After turning the edges of the sheet, the dimensions will be x and 10 - 2x, so the cross-sectional area will be:

In order to maximize this area, let's find the x-coordinate of the vertex, using the formula:
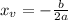
Where a and b are coefficients of the quadratic function in the standard form:
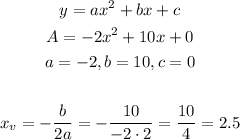
So the depth of the gutter is 2.5 inches.
And the maximum cross-sectional area is: