Given a circle with centre o and inscribed 8 identical triangles with radius 10cm
(a) To Determine: The size of angle AOB
Solution:
Note that all the 8 identical tringles divide the circle into 8 equal parts with 8 equal angles.
Also note that sum of angle at the centre of the circle is 360 degrees
Given that one of the angle is angle AOB, then
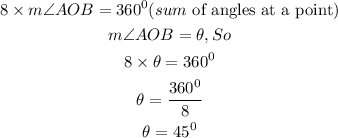
Hence, angle AOB is equal to 45⁰
(b) To Determine: The total area of the shaded regions
The area of the shaded region is
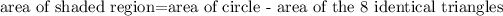
![\begin{gathered} A_{\text{circle}}=\pi r^2;r=10\operatorname{cm} \\ A_{\text{circle}}=\pi*10^2 \\ A_{\text{circle}}=100\pi \\ A_{\text{circle}}=314.1592654\operatorname{cm}^2 \end{gathered}]()
![\begin{gathered} A_{\text{triangles}}=(1)/(2)r^2\sin \theta \\ A_{\text{triangles}}=(1)/(2)*10^2*\sin 45^0 \\ A_{\text{triangles}}=(1)/(2)*100*0.7071 \\ A_{\text{triangles}}=35.35533908\operatorname{cm}^2 \\ A_{8\text{triangles}}=8*35.35533908\operatorname{cm} \\ A_{8\text{triangles}}=282.8427125\operatorname{cm}^2 \end{gathered}]()
![\begin{gathered} A_{\text{shaded region}}=A_(circle)-A_(8triangles) \\ A_{\text{shaded region}}=314.1592654\operatorname{cm}-282.8427125\operatorname{cm}^2 \\ A_{\text{shaded region}}=31.31655\operatorname{cm}^2 \\ A_{\text{shaded region}}=31.3\operatorname{cm}^2(3\text{significant figure)} \end{gathered}]()
Answer Summary:
(a) The size of angle AOB is 45⁰
(b) The total area of the shaded region correct to 3 significant figures is 31.3cm²